snowdeer's Code Holic

우분투(Ubuntu) 16.04 한글 키보드 설치

21 Jan 2018 | 리눅스 설정 Ubuntu

한글 키보드 설치

Ubuntu 16.04 LTS 버전 기준으로 한글 키보드를 설치하는 방법입니다.

먼저 아래의 명령어를 수행해서 fcitx-hangul 패키지를 설치합니다.

sudo apt-get install fcitx-hangul

그리고 아래의 절차를 진행합니다.

  • System Settings 실행
  • Language Support 아이콘 실행
  • 언어팩을 설치하라는 팝업창이 뜨면 ‘설치’ 선택
  • ‘Keyboard input method system’ 항목을 fcitx로 변경
  • 재부팅


오른쪽 한/영키(Alt 키)를 이용한 한/영 전환

Unbuntu에서는 기본적으로 오른쪽 Alt 키가 커맨드 실행 기능으로 맵핑이 되어 있습니다. 한/영 전환 키로 활용하고 싶으면 다음과 같이 세팅하시면 됩니다.

  • System Settings에서 Keyboard 실행
  • Shortcuts 탭 선택한 후 Typing 항목 선택
  • 모든 항목(Switch to next source, Switch to previous source, Alternative Characters Key)을 Disabled로 설정(Back 키를 누르면 Disabled가 됨)
  • Compose Key 항목을 Right Alt로 변경
  • Switch to next source를 선택한 다음 오른쪽 Alt 키(한/영 키)를 누르면 Multikey라는 항목으로 값이 설정됨


fcitx 설정

  • 오른쪽 상단 상태바에서 fcitx 아이콘 선택 → Configure Current Input Method 선택
  • + 버튼을 눌러 Hangul 항목 추가(+ 버튼 누른 창에서 Only Show Current Language 체크 버튼 해제해야 보임)
  • Global Config 탭으로 변경하여 Trigger Input Method 항목을 한/영 키로 설정(Multikey라고 표현됨)
  • Extra key for trigger input method는 Disabled

Visual Studio Code에 Go 개발 환경 세팅

21 Jan 2018 | Go

Visual Studio Code에 Go 개발 환경 세팅

Visual Studio Code(이하 vscode)에서 Go 언어 개발 환경 세팅 방법을 포스팅 해봅니다.


go 플러그인 설치

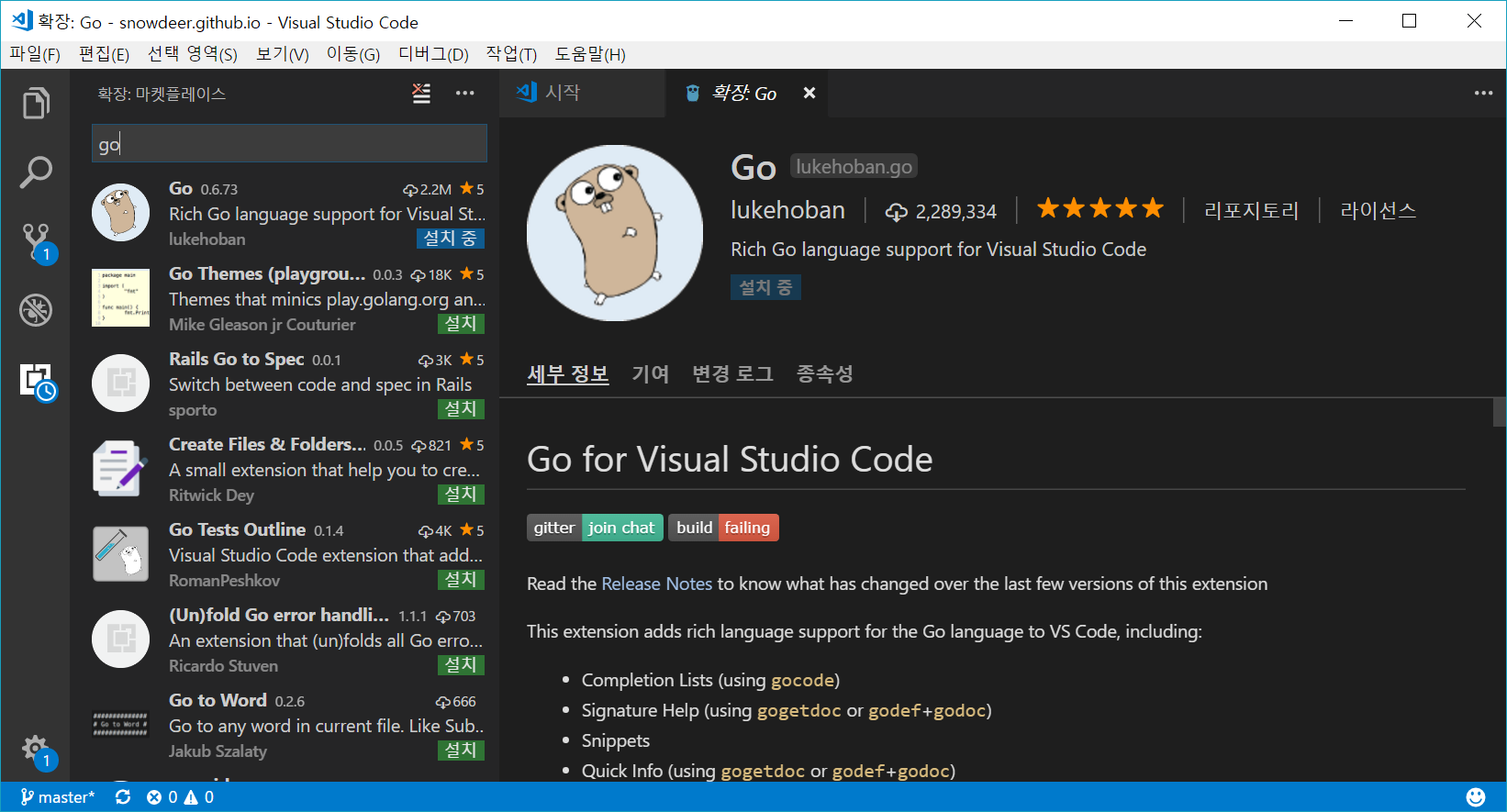
Image

먼저 vscode에서 위 이미지와 같이 ‘go’ 플러그인을 설치합니다.


개발 디렉토리 설정

그리고 소스를 관리할 개발용 디렉토리를 설정합니다. 저같은 경우는 Windows에서는 C:\Workspace\vscode_go로 세팅했고, Linux에서는 /home/snowdeer/Workspace/go 아래에 설정했습니다.

그리고 GOPATH 환경 변수 설정을 해야 합니다. Windows에서는

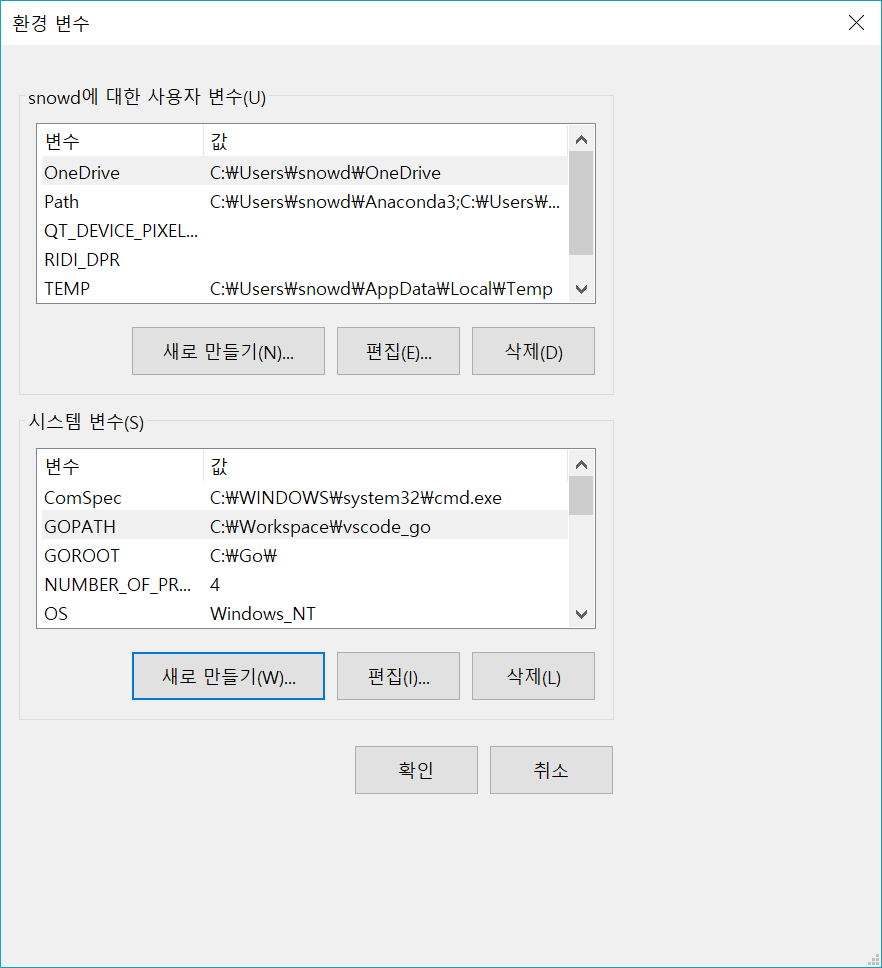
Image

환경 변수 편집 화면에서 GOPATH 항목을 등록해주면 되고, Linux에서는 터미널에서 export 명령어를 이용하면 됩니다.

export GOPATH="/home/snowdeer/Workspace/go"

그리고 해당 디렉토리에는 각각 src, pkg, bin 이름의 하위 디렉토리를 만들어줍니다.


추가 파일 설치

이제 vscode에서 Go 프로그래밍을 위한 실행 파일들을 다운로드하고 설치하는 작업을 합니다. 위에서 만든 디렉토리의 src 폴더 아래에 main.go 파일을 작성하고 vscode에서 열어봅니다.

그러면 vscode에서 아래 이미지와 같이 필요한 파일들을 설치할 것인지를 물어볼 것입니다.

Image

그냥 Install All을 선택해서 모든 파일들을 설치하면 됩니다. 모든 파일들을 설치하는데는 약 5분 정도의 시간이 걸릴 수 있습니다.

Installing 9 tools at C:\Workspace\vscode_go\bin
  gopkgs
  go-outline
  go-symbols
  guru
  gorename
  godef
  goreturns
  golint
  dlv

Installing github.com/uudashr/gopkgs/cmd/gopkgs SUCCEEDED
Installing github.com/ramya-rao-a/go-outline SUCCEEDED
Installing github.com/acroca/go-symbols SUCCEEDED
Installing golang.org/x/tools/cmd/guru SUCCEEDED
Installing golang.org/x/tools/cmd/gorename SUCCEEDED
Installing github.com/rogpeppe/godef SUCCEEDED
Installing sourcegraph.com/sqs/goreturns SUCCEEDED
Installing github.com/golang/lint/golint SUCCEEDED
Installing github.com/derekparker/delve/cmd/dlv SUCCEEDED

All tools successfully installed. You're ready to Go :).


테스트 코드 및 실행

다음 코드로 실행 테스트를 해봅니다.

package main

import "fmt"

func main() {
	fmt.Println("Hello, snowdeer")
	fmt.Println("안녕. 스노우디어")
}

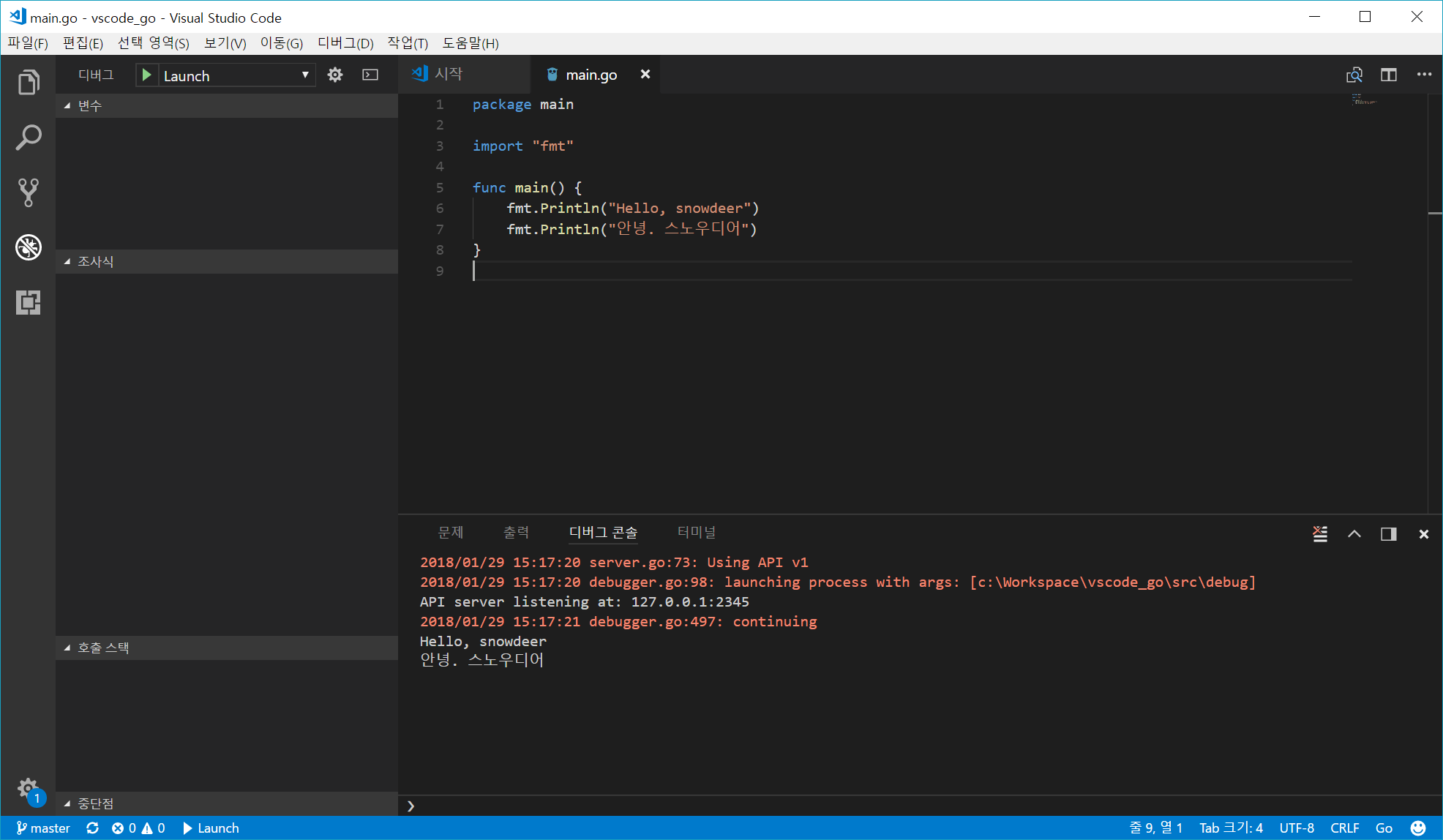
코드 작성 후 F5 키를 눌러 실행을 해봅니다. 브레이크 포인트(Break Point)를 걸고 디버깅을 해볼 수도 있습니다.

Image

CentOS 7에 Go 언어 설치하기

20 Jan 2018 | Go

Install Golang on CentOS 7

CentOS 7 기준으로 Go 언어를 설치하는 방법입니다.


Go 언어 다운로드

먼저 현재 릴리즈되어 있는 Go 언어 패키지 다운로드 주소를 여기에서 확인합니다.

$ wget https://dl.google.com/go/go1.10.linux-amd64.tar.gz


Go 언어 설치

위에서 받은 tar 파일의 압축을 풀어줍니다.

$ sudo tar -C /usr/local -xvzf go1.10.linux-amd64.tar.gz

그리고 작업하고자하는 디렉토리에 아래 디렉토리들을 생성해줍니다. (저같은 경우는 /home/snowdeer/go/ 디렉토리 아래에서 작업합니다.)

$ mkdir bin

$ mkdir pkg

$ mkdir src


환경 변수 설정

/etc/profile.d/path.sh 파일을 열고 아래 내용을 저장합니다.

export PATH=$PATH:/usr/local/go/bin

또한 /home/snowdeer/.bash_profile 파일에도 다음 라인을 추가합니다.

export GOBIN="$HOME/go/bin"
export GOPATH="$HOME/go"

또한 기존의 PATH 변수에 GOBIN 경로도 추가해줍니다.

그런다음 터미널에서 다음 명령어를 입력해서 환경 변수를 시스템에 적용합니다.

$ source /etc/profile

$ source ~/.bash_profile


설치 확인

다음 예제 코드를 실행해서 Go 언어가 잘 동작하는지 확인합니다.

package main

import "fmt"

func main() {
    fmt.Printf("Hello, World!\n")
}

그 이후 터미널에서 다음 명령어를 실행해봅니다. (아무거나 실행해봐도 됩니다.)

$ go run hello.go

$ go build hello.go

$ go install hello.go

Ubuntu에 Go 언어 설치하기

19 Jan 2018 | Go

Ubuntu에 Go 언어 설치하는 방법

Go 언어 공식 다운로드는 https://golang.org/dl/에서 할 수 있습니다.

또는 Ubuntu 기준으로 다음 명령어로 Go 언어를 설치할 수도 있습니다.


apt-get을 이용한 설치

$ sudo apt-get install golang-go

만약 너무 오래된 버전의 Go 언어가 설치될 경우 다음 명령어로 좀 더 최신 버전의 Go 언어를 설치할 수도 있습니다. (Ubuntu 16.04 LTS 버전의 경우는 아래쪽 포스팅 내용을 따르세요.)

$ sudo add-apt-repository ppa:gophers/archive

$ sudo apt-get update

$ sudo apt-get install golang-1.9-go

참고로 golang-1.9-go 패키지의 바이너리는 /usr/lib/go-1.9/bin 위치에 설치됩니다.


snap을 이용한 설치

snap을 이용할 경우 다음 명령어를 이용해서 최신 버전의 Go 언어를 설치할 수 있습니다.

$ snap install --classic go


Ubuntu 16.04 에서의 설치

Ubuntun 16.04에서는 golang-1.9-go 패키지를 설치 못하는 경우가 발생할 수 있습니다. 이런 경우는 다음 명령어를 이용해서 설치합니다.

$ sudo add-apt-repository ppa:longsleep/golang-backports

$ sudo apt-get update

$ sudo apt-get install golang-go

RNN(Recurrent Neural Network)

18 Jan 2018 | 머신러닝

순환 신경망

RNN(Recurrent Neural Network)는 시리(Siri), 빅스비(Bixby) 등 언어 인식에 많이 활용되고 있습니다. 사람의 언어를 이해한다는 것은 앞뒤 단어와 같이 과거에 입력된 데이터들의 관계를 고려해서 이해할 수 있다는 뜻입니다.

순환 신경망은 여러 개의 데이터가 순서대로 입력되었을 때 앞서 입력받은 데이터를 잠시 기억해 놓는 방법입니다. 그리고 기억된 데이터의 중요도를 판별하여 별도의 가중치를 부여한 다음 다음 데이터로 넘어갑니다. 모든 입력 값에 대해 이 작업을 순서대로 실행하는데, 마치 다음 층을 가기 전에 같은 층을 계속해서 맴도는 것처럼 보이기 때문에 순환 신경망이라고 부릅니다.

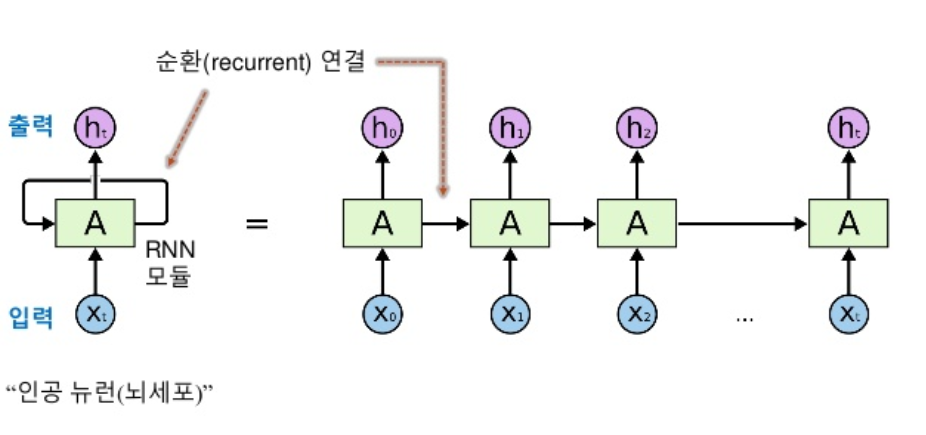
Image


순환 신경망의 활용

  • 음성 인식기
  • 번역기
  • 사진을 보고 캡션 추가하기
  • 펜으로 필기하는 과정을 RNN으로 학습하여 필기를 텍스트로 인식하거나 텍스트를 필기체로 변환
  • 음악 일부를 듣고 이어서 음악 재생하기


순환 신경망 예제

Google Quick, Draw!

Image

사람이 그린 그림을 보고 구글에서 무엇을 그린 건지 맞추는 웹사이트입니다. 재미로 해볼만한데 꽤 괜찮은 성능을 보여줍니다.


LSTM

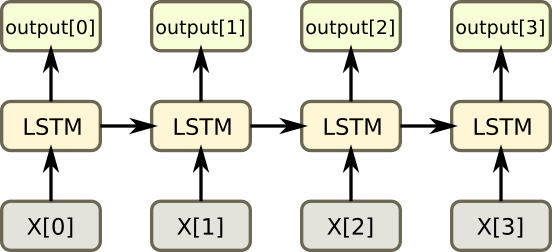
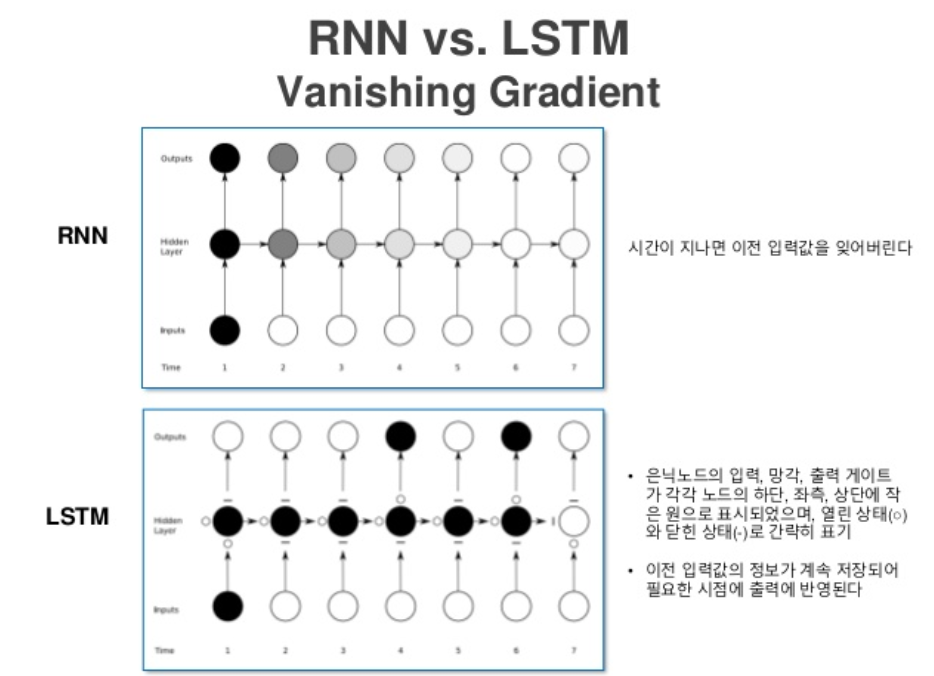
LSTM(Long Short Term Memory)은 RNN의 성능을 더욱 개선하기 위해서 여러가지 연구가 계속되다가 나온 방법 중 하나입니다.

RNN은 한 층 안에서 반복을 계속하기 때문에 경사각소실(Vanishing Gradient)이 발생하기 쉽고, LSTM은 이를 보안한 방법입니다. 반복되기 직전에 다음 층으로 기억된 값을 넘길지 안 넘길지 관리하는 단계를 하나 더 추가하는 방법입니다.

Image

Image