알고리즘 공부를 하다보면 간단한 정렬 알고리즘 하나 정도는 알아두는 편이 좋습니다. 그런데, 정렬 알고리즘들은 정말 다양하게 존재합니다. 물론, 성능도 제각각입니다. 그럼 어떤 알고리즘을 알아두는 것이 좋을까요?

보통 후보로 뽑히는 알고리즘은 Quick Sort 또는 Merge Sort입니다. 둘 다 분할 정복(Divide & Conquer) 기반 알고리즘이며 성능도 O(N log N)으로 비슷합니다. 취향에 따라 선택하면 되지만, Merge Sort가 좀 더 구현하기 쉬워서 개인적으로는 후자를 추천합니다.

Quick Sort와 Merge Sort를 비교해보면 다음과 같습니다.

• Quick Sort는 Worst Case에서 O(N^2)의 속도를 가진다.
• Merge Sort는 Worst Case에서도 O(N log N) 속도를 유지한다.
• 대신 Merge Sort는 더 큰 메모리 공간이 필요하고 메모리 할당/복사/삭제가 빈번해서 Quick Sort보다 속도가 좀 더 느린 경우도 종종 있다. (평균적으로는 비슷하다.)
• Merge Sort는 같은 값들의 순서가 정렬 후에도 유지되는 stable 한 성격을 갖고 있고, Quick Sort는 그러지 않다.

참고로 C++ 표준 라이브러리인 STL 에서는 2가지의 sort 함수를 제공하고 있는데, 일반적인 sort는 Quick Sort, stable_sort는 Merge Sort를 사용하고 있다고 합니다.

자, 그럼 MergeSort에 대해서 단계적으로 살펴보도록 하겠습니다.

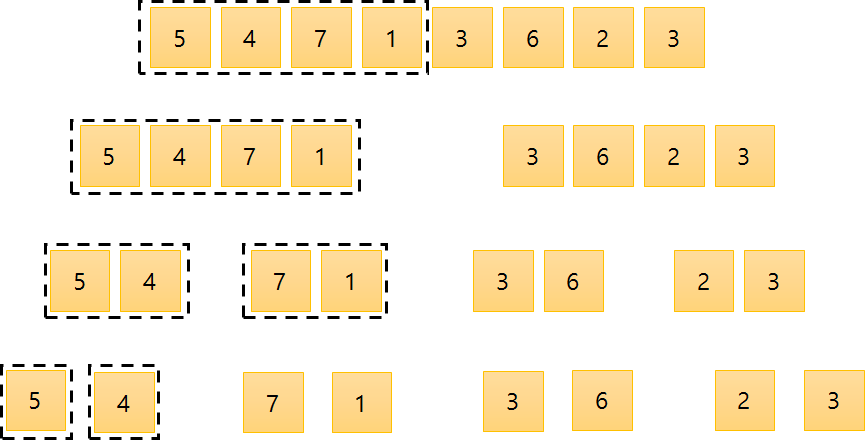
분할

분할 정복 기반의 알고리즘이기 때문에 일단 분할을 합니다. 다음과 같이 1/2씩 나누기만 하면 됩니다.

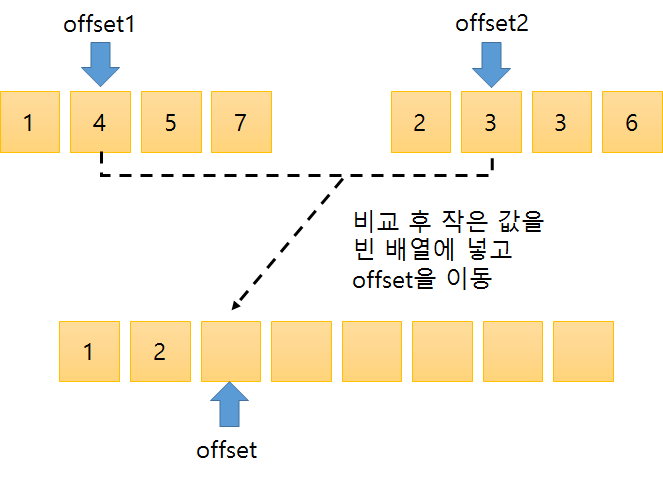
정합

이렇게 나누어진 값들을 이제 합치면서 정렬을 해줍니다.

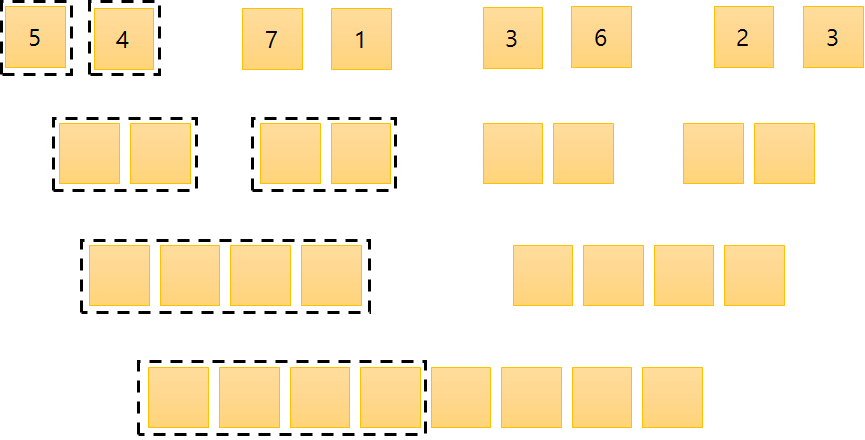정렬 방법은 다음과 같습니다.

코드

실제 코드로 확인해보도록 하겠습니다. 다음은 C++ 코드입니다.

int temp[MAX];

void mergeSort(int*arr, int left, int right) {
  // 종료 조건: 나눌 수 없을 때까지 나눈다.
  if(left >= right) {
    return;
  }

  // 분할
  int mid = (left + right) / 2;
  mergeSort(arr, left, mid);
  mergeSort(arr, mid + 1, right);

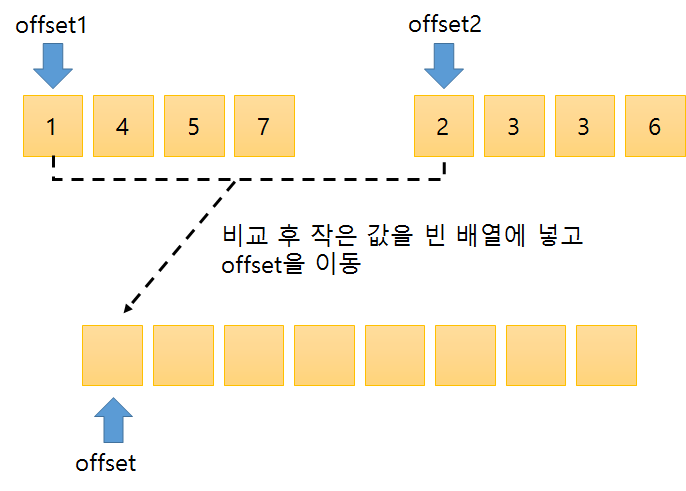
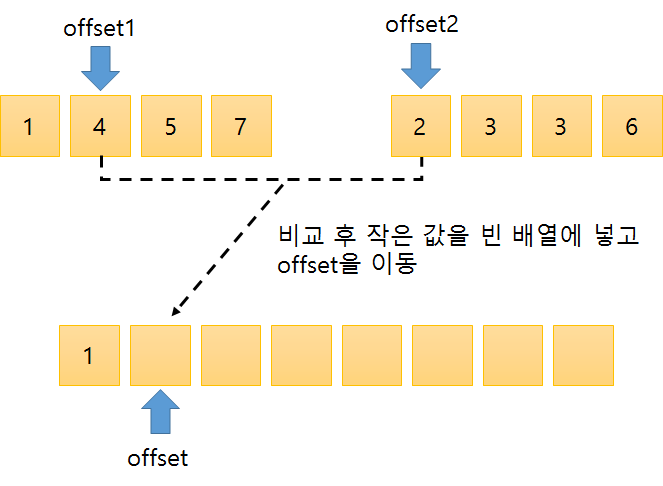
  // 정합
  int length = right - left + 1;
  int offset = 0, offset1 = left, offset2 = mid + 1;

  while((offset1 <= mid) || (offset2 <= right)) {
    if(offset1 > mid) {
      temp[offset++] = arr[offset2++];
      continue;
    }
    if(offset2 > right) {
      temp[offset++] = arr[offset1++];
      continue;
    }
    if(arr[offset1] <= arr[offset2]) {
      temp[offset++] = arr[offset1++];
      continue;
    } else {
      temp[offset++] = arr[offset2++];
      continue;
    }
  }

  for(int i = 0; i < length; i++) {
    arr[left + i] = temp[i];
  }
}