Heap 이란

부모 노드의 값은 자식 노드의 값보다 항상 크다(또는 작다)라는 규칙을 갖고 있는 트리(Tree) 형태의 자료 구조를 Heap 이라고 합니다.

크게 Max Heap과 Min Heap으로 나누어집니다. Max Heap은 부모 노드의 값이 항상 자식 노드의 값보다 큰 규칙을 갖고 있으며, Min Heap은 그 반대입니다.

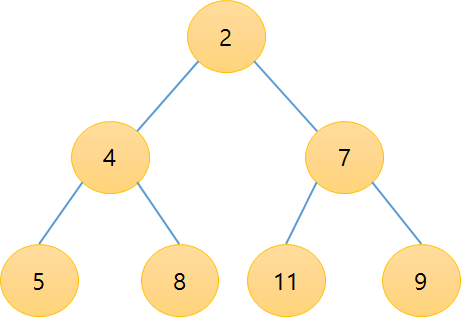
Heap의 성격상 최상위 노드인 root 노드에는 데이터 중에서 가장 큰(작은) 값이 저장됩니다. 즉, Heap에서 데이터를 하나씩 꺼내게 되면 정렬과 같은 효과를 가지는데, 이러한 정렬을 힙 정렬(Heap Sort)라고 합니다. 성능은 O(N log N)입니다.

특징

Heap은 이진 트리(Binary Tree) 형태로 이루어져 있습니다. 그리고 이진 트리 중에서도 완전 이진 트리(Complete Binary Tree)입니다.

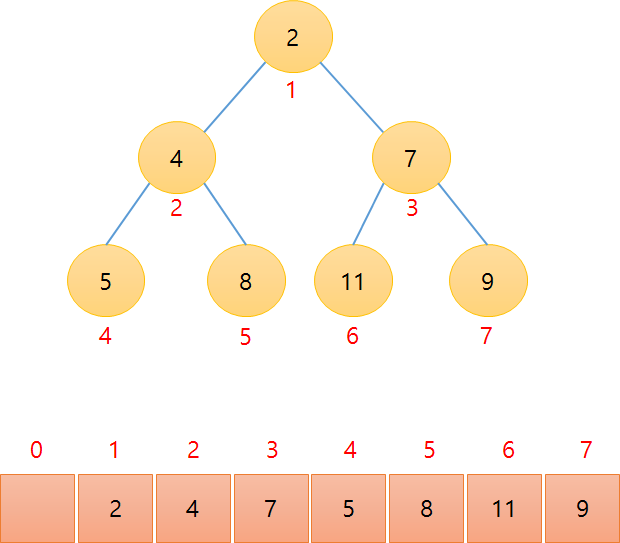
완전 이진 트리라는 특징(앞에서부터 차례대로 채워지는 규칙) 때문에 Heap을 구현할 때,  트리보다 배열을 이용하는 경우가 많습니다. 위에서 예제로 그린 트리를 배열로 나타내면 다음과 같습니다.

배열 칸에 값이 들어가며, 위쪽에 있는 숫자는 배열 칸의 인덱스입니다. 배열은 0부터 시작해도 되고, 1부터 시작해도 됩니다. 다만, 그 공식이 살짝 바뀌긴 하는데 큰 차이는 없습니다. 저같은 경우는 그냥 1부터 시작하는게 습관이 되어서 주로 0번째 배열은 1번째 배열부터 채워나가는 편입니다.

배열 칸의 인덱스와 트리안의 노드들과의 관계는 다음과 같습니다.

이제 부모 노드와 자식 노드간의 관계를 유추할 수 있습니다. 그 관계는 다음과 같습니다.

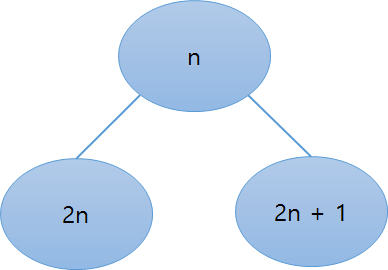
자식 노드의 인덱스를 2로 나누면 부모 노드의 인덱스가 되고, 반대로 부모 노드에서 왼쪽 자식 노드는 2를 곱한 값, 오른쪽 자식 노드는 2를 곱한 값에 1을 더한 값을 인덱스로 가지게 됩니다. (배열의 시작을 0으로 하느냐, 1로 하느냐에 따라 이 공식은 달라집니다.)

• 부모 노드 인덱스 = (자식 노드 인덱스) / 2
• 왼쪽 자식 노드 인덱스 = (부모 노드 인덱스) x 2
• 오른쪽 자식 노드 인덱스 = (부모 노드 인덱스) x 2 + 1

코드

Heap 정의

static const int MAX_HEAP_SIZE = 1000;
class Heap {
public:
    Heap() {
        size = 0;
    }

    // Heap의 함수는 데이터의 삽입/삭제 2개가 필요하다.
    void push(int value);
    int pop();

private:
    int data[MAX_HEAP_SIZE];
    int size;

    void swap(int pos1, int pos2) {
        int temp = data[pos1];
        data[pos1] = data[pos2];
        data[pos2] = temp;
    }
};

구현

// 데이터 삽입은 쉽다.
// 배열의 가장 마지막 칸에 데이터를 넣은 다음,
// 부모 노드들과 비교해나가면서 부모가 자식보다 값이 더 크면
// 교환을 해주면 된다.
void Heap::push(int value) {
    size++;
    data[size] = value;

    int pos = size;
    while (true) {
        if (pos == 1) break;

        int parent_idx = pos / 2;
        int parent_value = data[parent_idx];

        if (parent_value <= data[pos]) {
            break;
        }

        swap(parent_idx, pos);
        pos = parent_idx;
    }
}

// 데이터 삭제는 복잡하다.
// 배열의 첫번째 인덱스 값을 리턴하는 것은 단순하게 되지만
// 그러면서 Heap을 재구성하는 것이 조금 복잡하다.
// 현재 비어 있는 칸의 왼쪽 자식과 오른쪽 자식의 값을 비교해서
// 더 작은 값을 비어 있는 칸으로 옮기는 작업을 반복적으로
// 수행하면 된다.
int Heap::pop() {
    if (size <= 0) return -1;
    int ret = data[1];
    data[1] = data[size];
    size--;

    int pos = 1;
    while (true) {
        int left_child_idx = pos * 2;
        int right_child_idx = pos * 2 + 1;

        if (left_child_idx > size) break;

        // child node 가 1개인 경우와 2개인 경우를 나누어 처리
        if (right_child_idx > size) {
            int left_child_value = data[left_child_idx];
            if (left_child_value >= data[pos]) {
                break;
            }
            swap(left_child_idx, pos);
            pos = left_child_idx;
        }
        else {
            int left_child_value = data[left_child_idx];
            int right_child_value = data[right_child_idx];

            if ((left_child_value >= data[pos]) && (right_child_value >= data[pos])) {
                break;
            }

            if (left_child_value <= right_child_value) {
                swap(left_child_idx, pos);
                pos = left_child_idx;
            }
            else {
                swap(right_child_idx, pos);
                pos = right_child_idx;
            }
        }
    }

    return ret;
}

Heap을 쓰는 경우가 많지는 않지만 가끔씩 요긴하게 쓰일 때가 있습니다. 대표적으로 우선 순위 큐(Priority Queue)를 들 수 있겠네요. 우선 순위 큐는 최단 경로 찾기 알고리즘(ex. Dijkstra) 등에서 활용되고 있습니다.