세그먼트 트리(Segment Tree)는 구간별 최대값, 최소값 등을 빠르게 구할 수 있게 해주는 트리 형태의 데이터 구조입니다.

Segment Tree 구조

Segment Tree는 완전 이진 트리이며, 부모 노드는 각 자식 노드들의 범위에 대한 정보를 갖고 있습니다. 각 노드간의 관계는 아래와 같습니다.

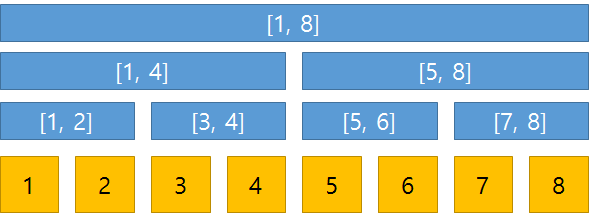
실제 데이터는 맨 아래의 Leaf 노드들이 가지게 되며, 부모 노드들은 각각의 자식 노드들의 구간내의 정보를 갖게 됩니다. 예를 들어, 구간 내 최소값을 관리하는 Segment Tree를 알아보도록 하겠습니다.

구간별 최소값을 관리하는 Segment Tree

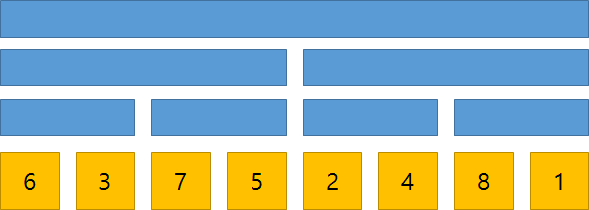
실제 데이터는 대략 이런 식으로 저장이 됩니다. (최하위 노드에만 값이 저장됩니다.) 이 때, 부모 노드들에 들어갈 값들을 살펴보도록 하겠습니다.

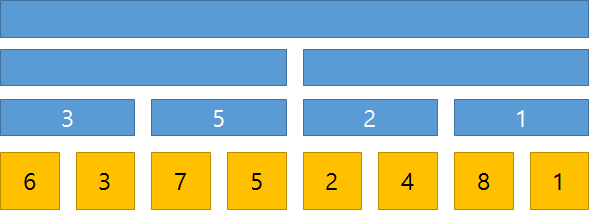
이런 식으로 각 부모 노드들은 해당 구간에 속하는 자식 노드들의 최소값을 저장하게 되며,

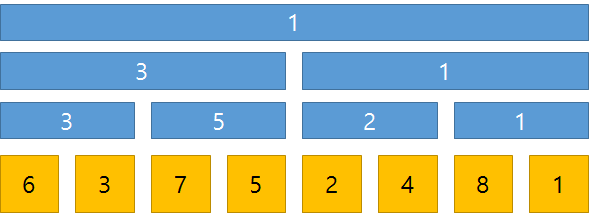
차곡차곡 각 부모 노드들의 데이터가 채워지게 됩니다.

구간별 최소값 조회

이제, Segment Tree를 이용한 구간별 최소값 조회를 한 번 해보도록 하겠습니다. 예를 들어, 1번째 노드부터 7번째 노드까지의 최소값을 구해보겠습니다.

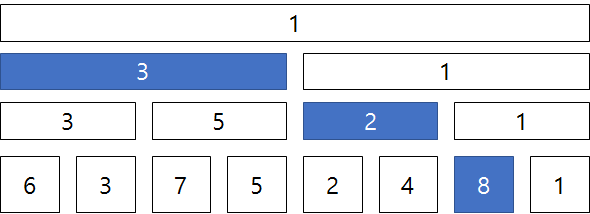원래는 1번째 노드부터 7번째 노드까지 차례대로 값을 확인해야 했지만, Segment Tree에서는 위 그림과 같이 3개의 노드만 검색을 하면 최소값을 얻을 수 있습니다. 데이터 사이즈가 커지면 더욱 속도 차이가 많이 나게 될 것입니다.

데이터 갱신

데이터 갱신을 할 경우 Segment Tree는 해당 범위를 포함하고 있는 모든 부모 노드들의 값을 다시 업데이트해줘야 합니다.

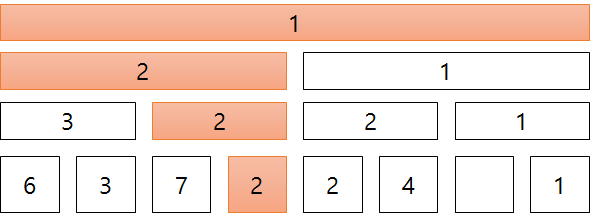
만약 4번째 노드의 값이 변경될 경우, 이런 식으로 4번째 노드를 포함하고 있는 모든 부모 노드들의 값을 업데이트 해줘야 합니다.

코드

Segment Tree 정의

Segment Tree의 구조를 보면 실제 데이터보다 약 2배만큼의 저장 공간을 더 사용하고 있습니다. (실제 데이터 공간과 그 범위를 관리하는 부모 노드들의 공간을 합치면 약 2배가 됩니다.)

따라서 아래 코드와 같이 실제 데이터보다 2배 정도의 크기를 선언해서 사용하면 되고, 초기값은 무한대로 설정했습니다.

static const int MAX_TREE_SIZE = 100000;
static const int INFINITE = 9999999;
int data[] = { 0, 6, 3, 7, 5, 2, 4, 8, 1, };
int N = 8;
int segment_tree[2 * MAX_TREE_SIZE];

int getMin(int a, int b) {
    if (a <= b) return a;
    return b;
}

void initialize() {
    int size = 2 * N - 1;
    for (int i = 1; i <= size; i++) {
        segment_tree[i] = INFINITE;
    }
}

void debug() {
    int size = 2 * N - 1;
    int pow = 2;
    for (int i = 1; i <= size; i++) {
        printf("%d ", segment_tree[i]);
        if (i == (pow - 1)) {
            printf("\n");
            pow = pow * 2;
        }
    }

    printf("\n");
}

데이터 갱신

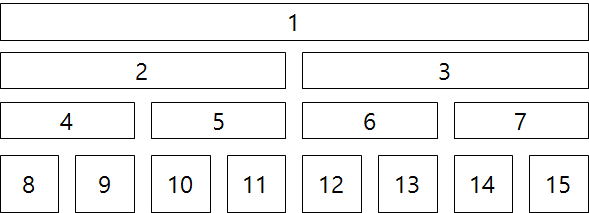
각 노드들에 인덱스를 매겨보면,

와 같이 인덱스를 붙일 수 있습니다. 부모 노드와 자식 노드간의 관계는 아래 그림과 같습니다.

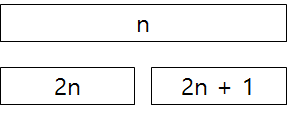
즉, 데이터 갱신은 다음과 같은 코드를 통해서 할 수 있습니다.

void update(int pos, int value) {
    pos = pos + (N -1);
    segment_tree[pos] = value;

    while (true) {
        pos = pos / 2;
        if (pos == 0) break;
        segment_tree[pos] =
            getMin(segment_tree[2 * pos], segment_tree[2 * pos + 1]);
    }
}

데이터 조회

데이터 조회 부분이 좀 복잡한데, 다음과 같은 재귀 함수를 이용해서 조회를 할 수 있습니다.

// left, right : 구하고자 하는 값의 범위
// segment_left, segment_right : 현재 Segment의 구간
// node_id : 현재 node의 index
int query(int left, int right, int segment_left,
    int segment_right, int node_id) {
    // 전혀 관련이 없으면 INFINITE 리턴
    if ((segment_right < left) || (segment_left > right))
        return INFINITE;

    // 만약 현재 구간이 구하고자 하는 값의 범위 안에 있으면 SegmentTree값 리턴
    if ((segment_left >= left) && (segment_right <= right))
        return segment_tree[node_id];

    // 현재 Segment의 중간점
    int mid = (segment_left + segment_right) / 2;

    int left_value = query(left, right,
        segment_left, mid, 2 * node_id);
    int right_value = query(left, right,
        mid + 1, segment_right, 2 * node_id + 1);

    return getMin(left_value, right_value);
}

전체 소스 코드

#include <stdio.h>

static const int MAX_TREE_SIZE = 100000;
static const int INFINITE = 9999999;
int data[] = { 0, 6, 3, 7, 5, 2, 4, 8, 1, };
int N = 8;
int segment_tree[2 * MAX_TREE_SIZE];

int getMin(int a, int b) {
    if (a <= b) return a;
    return b;
}

void initialize() {
    int size = 2 * N - 1;
    for (int i = 1; i <= size; i++) {
        segment_tree[i] = INFINITE;
    }
}

void debug() {
    int size = 2 * N - 1;
    int pow = 2;
    for (int i = 1; i <= size; i++) {
        printf("%d ", segment_tree[i]);
        if (i == (pow - 1)) {
            printf("\n");
            pow = pow * 2;
        }
    }

    printf("\n");
}

void update(int pos, int value) {
    pos = pos + (N -1);
    segment_tree[pos] = value;

    while (true) {
        pos = pos / 2;
        if (pos == 0) break;
        segment_tree[pos] =
            getMin(segment_tree[2 * pos], segment_tree[2 * pos + 1]);
    }
}

// left, right : 구하고자 하는 값의 범위
// segment_left, segment_right : 현재 Segment의 구간
// node_id : 현재 node의 index
int query(int left, int right, int segment_left,
    int segment_right, int node_id) {
    // 전혀 관련이 없으면 INFINITE 리턴
    if ((segment_right < left) || (segment_left > right))
        return INFINITE;

    // 만약 현재 구간이 구하고자 하는 값의 범위 안에 있으면 SegmentTree값 리턴
    if ((segment_left >= left) && (segment_right <= right))
        return segment_tree[node_id];

    // 현재 Segment의 중간점
    int mid = (segment_left + segment_right) / 2;

    int left_value = query(left, right,
        segment_left, mid, 2 * node_id);
    int right_value = query(left, right,
        mid + 1, segment_right, 2 * node_id + 1);

    return getMin(left_value, right_value);
}

int main(int argc, char** argv) {
    initialize();

    for (int i = 1; i <= N; i++) {
        update(i, data[i]);
    }

    // Segment Tree 출력
    debug();

    // 최소값을 구하고자 하는 구간 입력
    int left = 2;
    int right = 8;
    int value = query(left, right, 1, N, 1);
    printf("Minimum between %d and %d : %d\n",
        left, right, value);

    return 0;
}