Binary Indexed Tree는 이진수 값을 인덱스로 활용해서 구간별 최소/최대/합 등을 쉽게 구할 수 있게 해주는 트리 형태의 데이터 구조입니다.

Segment Tree vs Binary Indexed Tree

Segment Tree로부터 좀 더 발전된 트리이며, 개념도 비슷합니다. Segment Tree 보다 더 적은 데이터 공간을 필요로 하며 코드 구현이 더 쉽습니다.

다만 처음 이해하는 과정이 조금 복잡하여 Segment Tree의 개념부터 이해를 하고 도전을 하는 것이 좋을 것 같습니다.

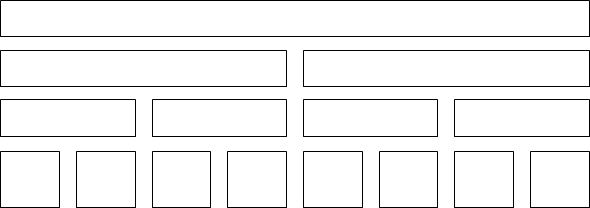
위의 그림은 어디서 많이 본 트리입니다. 바로 Segment Tree입니다. 여기서 잘 생각해보면 부모 노드는 어차피 자식 노드들의 정보로 이루어져 있기 때문에 중복된 데이터들이 존재하는 것을 알 수 있습니다.

예를 들어, 아래 예시와 같은 데이터가 있다면

왼쪽 자식 노드의 값 100, 오른쪽 자식 노드의 값 200
- 부모 노드는 자식 노드들의 값의 합이라고 하면 100 + 200 = 300
- 오른쪽 자식 노드가 없더라도 부모 노드의 값과 왼쪽 자식 노드의 값만 알면, 오른쪽 자식 노드의 값을 유추할 수 있음

즉, Segment Tree에서

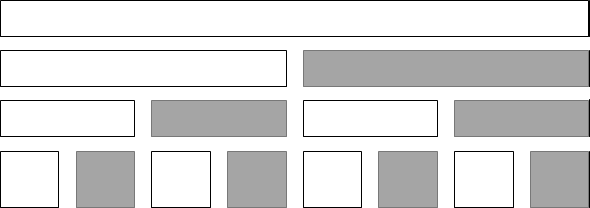회색 부분의 공간은 불필요한 공간이 되며,

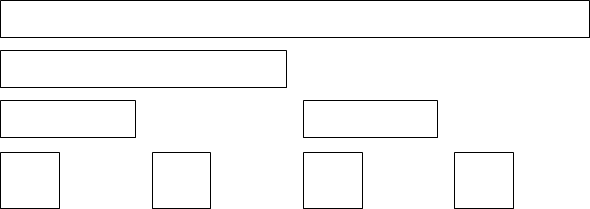와 같은 형태로 데이터 구조를 가져갈 수 있습니다.

Binary Indexed Tree 구조

실제로 값을 넣어보도록 하겠습니다.

실제 데이터는 대략 이런 식으로 저장이 된다고 가정 하면, Binary Indexed Tree는 다음과 같은 형태로 구성이 됩니다. (해당 구간의 데이터의 합을 구하는 Binary Indexed Tree라고 가정했습니다.)

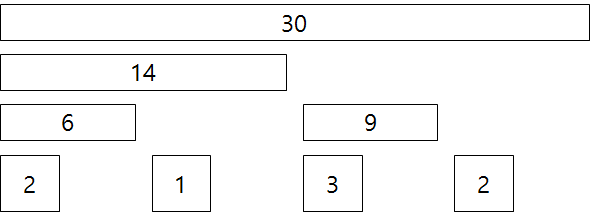다시 1차원 배열로 표현해보면 Binary Tree는

이 됩니다.

Binary Indexed Tree를 이용한 구간 합 구하기

Binary Indexed Tree를 이용하면 구간 합을 아주 빠르게 구할 수 있습니다. 예를 들어, 1 번째 노드부터 7 번째 노드까지의 구간 합은

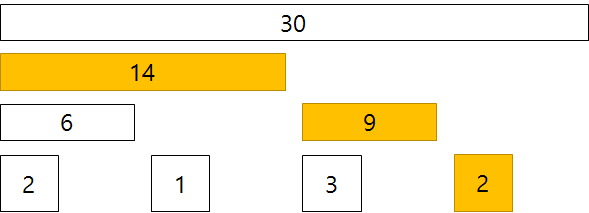와 같이 3개의 노드만 탐색하면 구할 수 있습니다.

Binary Indexed Tree의 노드 인덱스

Binary Indexed Tree의 각 노드별 인덱스를 구할 수 있으면, Binary Indexed Tree를 사용할 수 있는 준비는 거의 끝났다고 볼 수 있습니다.

각 노드마다 인덱스를 붙여보도록 하겠습니다.

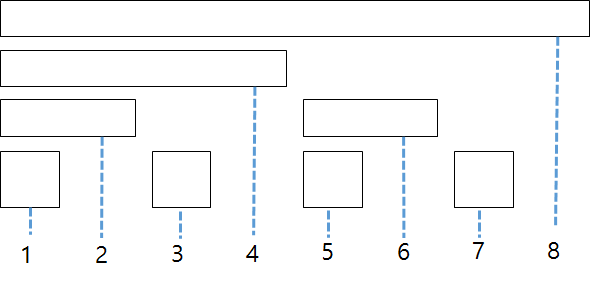이름 그대로 이진(Binary)법을 각 인덱스에 적용하면 다음과 같은 값이 되는데, 노드간 값을 잘 보면 규칙성이 있습니다.

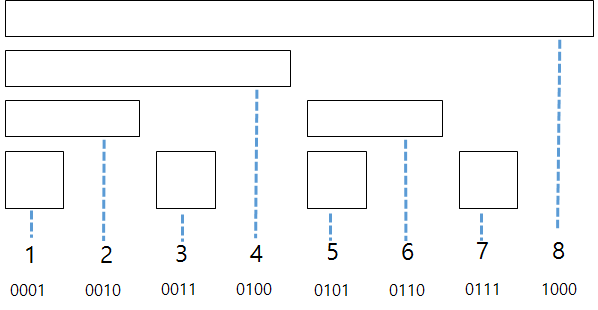예를 들어서, 노드 3번의 인덱스는 ‘0011’ 입니다. 노드 3번의 부모는 4번 노드로 인덱스는 ‘0100’ 입니다. 4번 노드의 부모는 8번 노드로 인덱스는 ‘1000’ 입니다.

예를 하나만 더 들어보도록 하겠습니다. 노드 5번의 인덱스는 ‘0101’ 입니다. 노드 5의 부모는 6번 노드이고, 인덱스는 ‘0110’ 입니다. 노드 6의 부모는 노드 8이며 인덱스는 ‘1000’ 입니다.

부모 노드와 자식 노드간의 규칙은 다음과 같습니다.

부모 노드의 인덱스는 자식 노드의 인덱스의 가장 마지막 '1' 값에 1을 더한 값

현재 이진 인덱스 값에서 가장 마지막에 위치한 ‘1’의 위치는 ‘index & (-index)’의 bit 연산을 통해서 얻을 수 있습니다. 즉, 현재 인덱스 값에 위의 ‘index & (-index)’ 값 을 더하면 부모 노드의 인덱스 값이 됩니다.

Binary Indexed Tree 값 업데이트 및 구간 합 구하기

Binary Indexed Tree에 값을 업데이트하거나 구간 합을 구하는 방법은 Segment Tree에서의 방법과 비슷합니다. Segment Tree와 마찬가지로 자식 노드의 값이 변경이 되면 부모 노드의 값들을 전부 업데이트해야 합니다.

그리고 자식과 부모 노드간의 관계는 앞에서 알아본 자식 노드 인덱스 가장 마지막 ‘1’ 값에 1을 더하는 방법으로 구할 수 있습니다.

값을 업데이트 할 때는 자식 노드부터 시작해서 가장 마지막 1 bit에 1을 더하면서 부모 노드를 찾아가서 값을 계속 갱신해주면 됩니다.

거꾸로 1부터 N 노드까지의 합을 구할 때는 N 노드부터 시작해서 가장 마지막 1 bit에 1을 빼면서 0이 될때까지 각 노드들의 합을 구하면 됩니다.

직접 코드로 확인해보도록 하겠습니다.

코드 (정의)

static const int MAX_TREE_SIZE = 100000;
static const int INFINITE = 9999999;
int data[] = { 0, 2, 4, 1, 7, 3, 6, 2, 5, };
int N = 8;
int bit[MAX_TREE_SIZE];

void initialize() {
    int size = 2 * N - 1;
    for (int i = 1; i <= size; i++) {
        bit[i] = 0;
    }
}

void debug() {
    for (int i = 1; i <= N; i++) {
        printf("%d ", bit[i]);
    }

    printf("\n");
}

코드 (데이터 갱신)

void update(int index, int value) {
    while (index <= N) {
        bit[index] = bit[index] + value;
        index = index + (index & (-index));
    }
}

코드 (1부터 N까지 구간 합)

int sum(int index) {
    int sum = 0;
    while (index > 0) {
        sum = sum + bit[index];
        index = index - (index & (-index));
    }

    return sum;
}

코드 (전체 소스 코드)

#include <stdio.h>

static const int MAX_TREE_SIZE = 100000;
static const int INFINITE = 9999999;
int data[] = { 0, 2, 4, 1, 7, 3, 6, 2, 5, };
int N = 8;
int bit[MAX_TREE_SIZE];

void initialize() {
    int size = 2 * N - 1;
    for (int i = 1; i <= size; i++) {
        bit[i] = 0;
    }
}

void debug() {
    for (int i = 1; i <= N; i++) {
        printf("%d ", bit[i]);
    }

    printf("\n");
}

void update(int index, int value) {
    while (index <= N) {
        bit[index] = bit[index] + value;
        index = index + (index & (-index));
    }
}

int sum(int index) {
    int sum = 0;
    while (index > 0) {
        sum = sum + bit[index];
        index = index - (index & (-index));
    }

    return sum;
}

int main(int argc, char** argv) {
    initialize();

    for (int i = 1; i <= N; i++) {
        update(i, data[i]);
    }

    // Binary Indexed Tree 출력
    debug();

    printf("Sum (1 ~ %d) : %d\n", 3, sum(3));
    printf("Sum (1 ~ %d) : %d\n", 5, sum(5));
    printf("Sum (1 ~ %d) : %d\n", 7, sum(7));

    return 0;
}