Perceptron

퍼셉트론은 1957년에 고안된 오래된 알고리즘이자, 딥러닝의 기원이 되는 알고리즘입니다.

퍼셉트론은 아래의 그림처럼 다수의 신호를 받아서 하나의 신호를 출력합니다. 이 때 출력값으로는 0 또는 1의 값만 가질 수 있습니다.

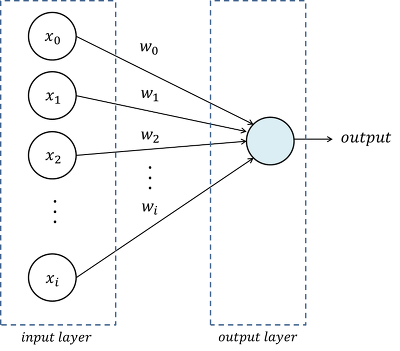
위 그림을 수식으로 표현하면

\[output = w_1 x_1 + w_2 x_2 + ... w_i x_i\]

가 되며, output은 0 또는 1의 값만 가지기 때문에 결과적으로 다음과 같은 식이 됩니다.

\[output = \begin{cases} 0 ( w_1 x_1 + w2 x_2 + ... + w_i x_i \le θ ) \\ 1 ( w_1 x_1 + w2 x_2 + ... + w_i x_i > θ ) \end{cases}\]

여기서 w 값은 가중치를 의미하며, $ θ $(theta)는 임계값이라고 합니다.

AND, OR, NAND 게이트

퍼셉트론을 이용하면 AND, OR, NOR 게이트 등을 아주 쉽게 만들 수 있습니다.

예를 들면 다음과 같습니다.

AND 게이트

$ x_1 $	$ x_2 $	y
0	0	0
1	0	0
0	1	0
1	1	1

이를 만족하는 ($ w_1 $, $ w_2 $, $ θ $) 조합은 (0.5, 0.5, 0.7), (1.0, 1.0, 1.0) 등 무수히 많은 조합이 나올 수 있습니다.

NAND 게이트

$ x_1 $	$ x_2 $	y
0	0	1
1	0	1
0	1	1
1	1	0

NAND 게이트는 AND 앞에 Not이 붙었기 때문에 ($ w_1 $, $ w_2 $, $ θ $) 조합을 간단히 (-0.5, -0.5, -0.7) 등과 같은 값을 입력해도 충분히 구현할 수 있습니다. 물론 조합의 경우의 수는 엄청 많습니다.

퍼셉트론 구현하기

퍼셉트론은 다음과 같이 간단한 코드로 구현할 수 있습니다. (Python 코드입니다.)

def AND(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.7
    value = x1 * w1 + x2 * w2
    if value <= theta:
        return 0
    elif value >= theta:
        return 1

bias 도입

\[output = \begin{cases} 0 ( b + w_1 x_1 + w2 x_2 + ... + w_i x_i \le 0 ) \\ 1 ( b + w_1 x_1 + w2 x_2 + ... + w_i x_i > 0 ) \end{cases}\]

위와 같이 기존의 퍼셉트론 수식에 b라는 값을 더해서 편향(bias)을 표현할 수 있습니다. 편향은 ‘한 쪽으로 치우쳐 균형을 깬다’는 의미를 갖고 있으며, 직선 그래프를 y축으로 b만큼 이동시키는 역할을 합니다.

$ w_1 $, $ w_2 $ 등의 가중치는 입력 신호가 결과값에 얼마나 큰 영향을 미치는지의 정도이며, b 값은 뉴런이 얼마나 쉽게 활성화하는지를 조절하는 매개변수입니다.

경우에 따라 b, $ w_1 $, $ w_2 $ 등을 전부 ‘가중치’라고 부르기도 합니다.

퍼셉트론의 한계

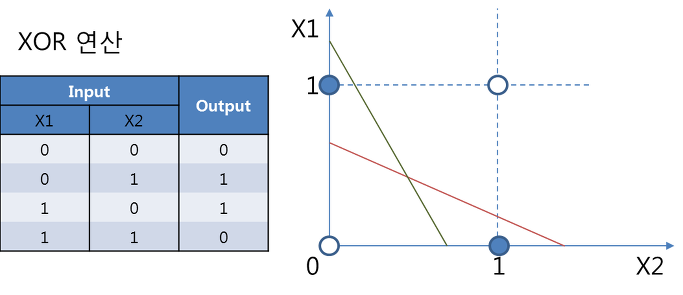
퍼셉트론을 이용하면 AND, OR, NAND 등의 게이트를 구현할 수 있었습니다. 하지만, XOR 게이트의 경우는 퍼셉트론만으로는 도저히 구현이 불가능합니다. 퍼셉트론은 직선으로 영역을 나누는데, XOR 게이트는 직선으로 영역이 나누어지지 않기 때문입니다.

다층 퍼셉트론

하지만 퍼셉트론을 여러 겹으로 층을 쌓은 다층 퍼셉트론(Multi-layer Perceptron)을 이용하면 XOR을 표현할 수 있습니다.

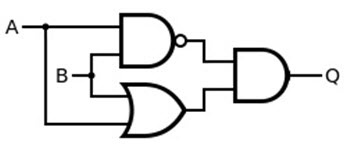
이를 Python 코드로 보면 다음과 같습니다.

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    result = AND(s1, s2)
    return result;

다층 퍼셉트론은 단층 퍼셉트론이 하지 못하는 복잡한 일들을 할 수 있습니다. 심지어 계산기나 컴퓨터까지 표현이 가능합니다.

snowdeer's Code Holic

퍼셉트론(Perceptron)