Activation Function

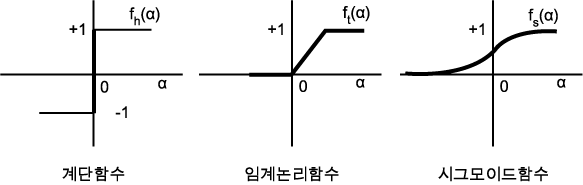
활성화 함수(Activation Function)는 신경망(Neural Network)에서 임계값(Threshold)을 이용해서 0 또는 1의 값을 출력하는 용도로 사용됩니다.

활성화 함수는 계단형 함수, 시그모이드(Sigmoid) 함수, ReLU 함수 등 다양한 함수가 사용되고 있습니다.

계단 함수

계단 함수는 다음과 같은 모습의 그래프로 표현됩니다.

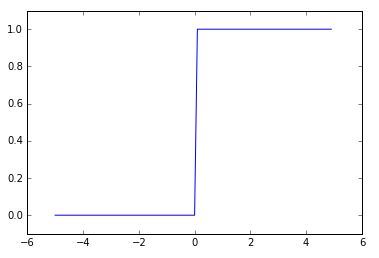
입력값이 특정 값 이상이면 1, 그렇지 않으면 0을 출력하는 평범한 함수입니다.

Sigmoid Function

시그모이드 함수는 다음과 같은 수식으로 되어 있습니다.

그래프로 표현하면 다음과 같습니다.

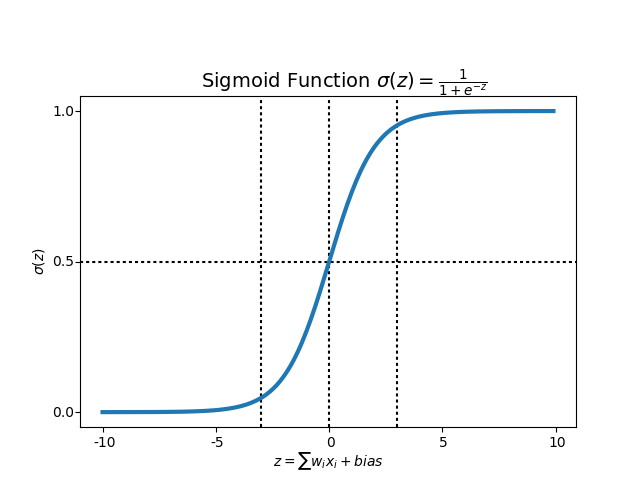
Python 코드로 표현하면 다음과 같이 작성할 수 있습니다.

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

계단 함수 vs 시그모이드 함수

계단 함수와 시그모이드 함수의 차이는 연속성에 있습니다. 계단 함수는 0과 1의 값이 특정한 값을 기준으로 갑자기 변합니다. 그 반면에 시그모이드 함수는 값이 연속적으로 매끈하게 이어집니다.

즉, 시그모이드 함수는 출력값이 0 또는 1의 값 뿐만 아니라 0.5, 0.7, 0.888 등의 실수값도 출력합니다.

계단 함수와 시그모이드 함수는 비슷한 점도 있습니다. 전체적인 모양으로 보면 둘은 비슷한 모양을 하고 있습니다. 입력값이 커질 수록 출력값은 1에 가까워지고, 반대의 경우는 0에 가까워집니다. 출력값이 0과 1 사이의 값이라는 것도 공통점입니다.

또한 두 함수는 ‘비선형 함수’라는 점도 동일합니다.

신경망에서는 활성화 함수로 비선형 함수만을 이용해야 합니다. 선형 함수는 신경망에서 계층을 깊게 하는 의미가 없어지기 때문입니다.

ReLU 함수

기존에는 활성화 함수로 계단 함수와 시그모이드 함수를 많이 사용했었습니다. 하지만 최근에는 ‘임계 논리 함수(ReLU, Rectified Linear Unit)’를 더 많이 사용하는 경향이 있습니다.

ReLU 함수는 입력이 0 이상이면 그 입력값을 그대로 출력하고, 그 이하에서는 0을 출력하는 함수입니다.

그래프로 표현하면 다음과 같습니다.

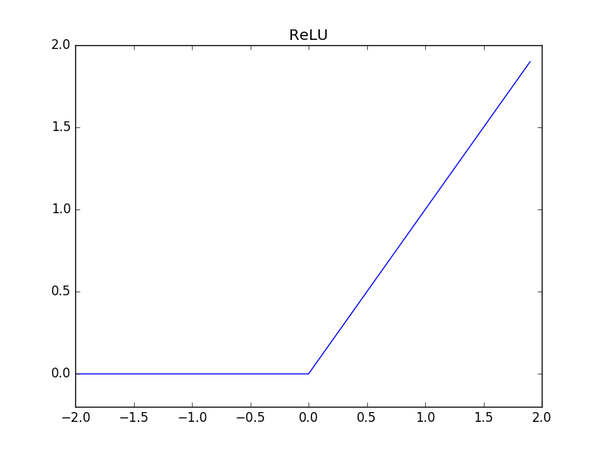
각 함수들의 그래프