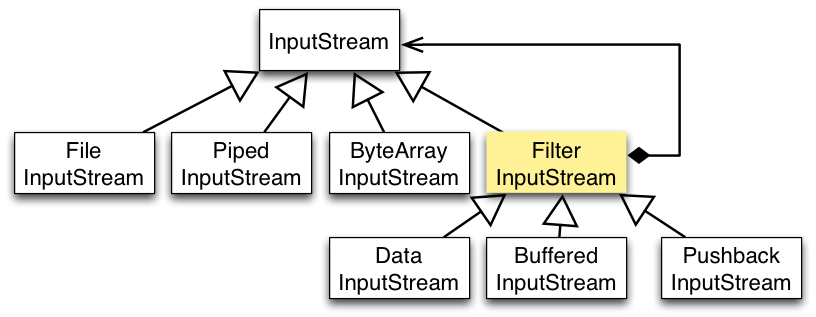
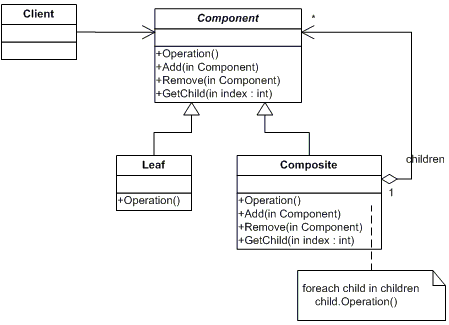
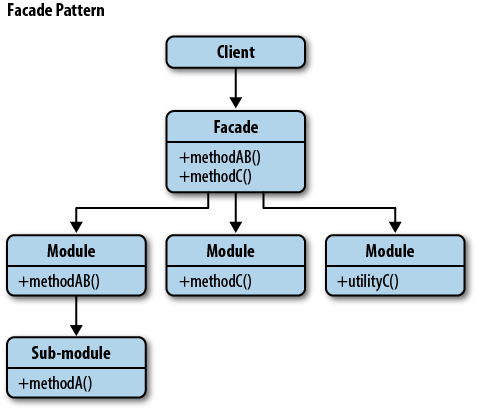
팩토리 메소드(Factory Method) 패턴
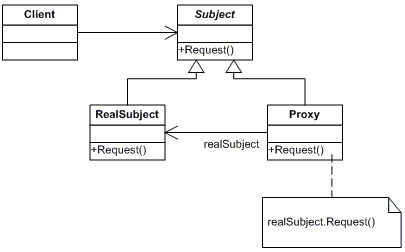
18 May 2016 | 디자인패턴팩토리 메소드(Factory Method) 패턴의 UML은 다음과 같습니다.
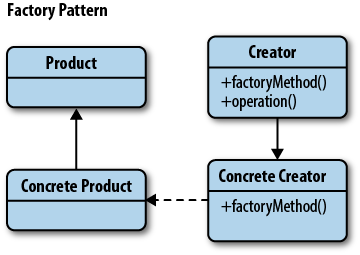
‘메소드’라는 단어를 생략하고 팩토리 패턴이라고도 불리우는 팩토리 메소드(Factory Method) 패턴에 대해서 알아보도록 하겠습니다.
Factory Method 패턴의 가장 큰 특징은 어떤 클래스의 인스턴스를 생성하는 방법을 바깥으로 노출시키지 않겠다는 것입니다. 인스턴스 생성은 서브 클래스에서 하게 되고 바깥에서는 Factory 역할을 하는 특정 클래스를 통해 해당 클래스의 인스턴스를 획득하게 됩니다.
예제 코드
예제를 보도록 하겠습니다.
public abstract class Pizza {
String mName;
String mDough;
String mSauce;
ArrayList<Topping> mToppingList = new ArrayList<Topping>();
public void prepare() {
System.out.println("Preparing " + mName);
System.out.println("Tossing dough...");
System.out.println("Adding sauce...");
System.out.println("Adding topping: ");
for(int i = 0; i < mToppingList.size(); i++) {
System.out.println(" " + mToppingList.get(i));
}
}
public void bake() {
System.out.println("Bake for 25 minutes");
}
public void cut() {
System.out.println("Cutting the pizza into diagonal slices");
}
public void box() {
System.out.println("Place pizza in official PizzaStore box");
}
public String getName() {
return mName;
}
}
이렇게 Pizza 라는 추상 클래스를 만들고, Pizza를 상속하는 다양한 Pizza 클래스를 만듭니다.
class CheesePizza extends Pizza {
// TODO
}
class PepperoniPizza extends Pizza {
// TODO
}
class ClamPizza extends Pizza {
// TODO
}
class VeggiePizza extends Pizza {
// TODO
}
그리고 Pizza를 만들어주는 추상 클래스인 PizzaStore를 만들도록 하겠습니다.
public abstract class PizzaStore {
public PizzaStore() {
}
Pizza orderPizza() {
Pizza pizza = createPizza();
pizza.prepare();
pizza.bake();
pizza.cut();
pizza.box();
return pizza;
}
abstract Pizza createPizza();
}
마찬가지로 PizzaStore를 상속받는 Concrete Class들을 만들어주면 됩니다.
class CheesePizzaStore extends PizzaStore {
@Override
Pizza createPizza() {
return new CheesePizza();
}
}
class PepperoniPizzaStore extends PizzaStore {
@Override
Pizza createPizza() {
return new PepperoniPizza();
}
}
이렇게 하면 각각의 PizzaStore에서 createPizza() 만 호출하면 그에 맞는 피자들의
인스턴스가 생성이 됩니다.