중재자(Mediator) 패턴은 Colleague들의 분쟁을 중간에서 중재해주는 클래스를 두고, 각 Colleague들끼리는 서로를 직접적으로 참조하지 못하도록 하여 낮은 결합도(Low Coupling)를 가지게 해주는 패턴입니다.

Colleague들끼리는 서로를 알지 못하기 때문에 특정 작업을 요청 하려면 무조건 Mediator에게 요청을 해야 합니다. 따라서 Mediator의 함수가 많아지고 코드량이 길어진다는 단점이 있습니다. 하지만, 결합도를 낮추어주기 때문에 향후 Colleague가 변경되거나 추가, 삭제될 때 유지 보수가 유리해진다는 장점이 있습니다.

Mediator 패턴의 UML은 다음과 같습니다.

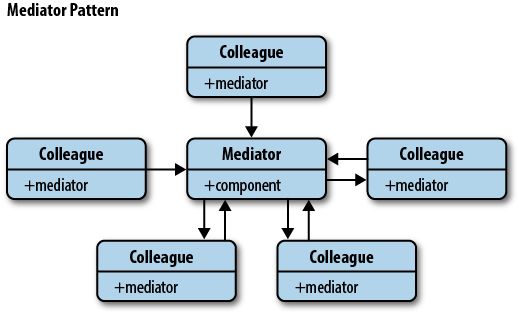
Mediator 패턴을 쓸 수 있는 경우는 다음과 같은 시나리오를 들 수 있습니다.

어떤 GUI 화면이 있다. 특정 체크박스의 값이 바뀌면 화면에 있는 각 버튼의 Enabled/Disabled 속성이 변경 된다. 또한, 텍스트 박스의 값에 따라 각 컴포넌트의 속성이 변경된다. 이와같이 각 컴포넌트들이 서로가 서로에게 영향을 미치는 경우이다.

위와 같은 경우 Mediator를 두지 않고, 각 버튼이나 체크 버튼, 텍스트 박스 등의 이벤트 처리 부분에서 각 컴포넌트의 속성을 직접 바꾸는 경우를 생각해 봅시다. 이 경우, 복수의 컴포넌트가 하나의 리소스에 동시에 작업 요청을 한다던지, 두 컴포넌트가 서로에게 작업 요청을 하여 무한 루프와 같은 데드락(Deadlock) 상황이 발생할 수도 있습니다. 또한 각 컴포넌트간이 참조가 많기 때문에 향후 특정 컴포넌트가 다른 컴포넌트로 교체하는 등의 유지보수가 쉽지 않다는 문제가 있습니다.

이런 경우 Mediator를 두고 각 상태에 따라 Mediator가 각 컴포넌트의 상태들을 변경시켜주게 되면 코드도 깔끔해지고 유지 보수도 수월할 수 있습니다.

예제 코드

Mediator 패턴은 크게 Mediator 인터페이스와 Colleague 인터페이스로 구성됩니다.

public abstract class Mediator {

  private ArrayList<Colleague> mColleagueList = new ArrayList<Colleague>();

  public void addColleague(Colleague colleague) {
    mColleagueList.add(colleague);
  }

  public void removeColleague(Colleague colleague) {
    mColleagueList.remove(colleague);
  }

  public void init() {
    for(Colleague colleague : mColleagueList) {
      colleague.init();
    }
  }

  public void fin() {
    for(Colleague colleague : mColleagueList) {
      colleague.fin();
    }
  }
}

public abstract class Colleague {

  private Mediator mMediator;

  public void setMediator(Mediator mediator) { mMediator = mediator; }

  public Mediator getMediator() { return mMediator; }

  public abstract void init();

  public abstract void fin();
}

그리고 Mediator와 Colleague를 상속(구현)받는 클래스들을 구현하면 됩니다.

스테이트(Command) 패턴은 오브젝트의 상태(State)를 클래스화한 패턴입니다.

스테이트 패턴을 사용하지 않았을 경우 만약 각 상태마나 다른 동작을 하게 하기 위해서 if 문을 사용했다면,

public void work() {
  if(현재 상태 == 낮){
    낮에 할 일();
  }
  else if(현재 상태 == 밤){
    밤에 할 일();
  }
}

와 같은 형태의 코드가 됩니다. 각 함수마다 현재 상태에 따라 분기문을 타게 되면, 향후 함수의 개수가 증가할 때마다(또는 상태가 증가할 때마다) 유지 보수가 힘들어지는 경우가 발생할 수 있습니다.

이런 경우 State 패턴을 사용하면 코드를 깔끔하게 관리할 수 있습니다. State 패턴의 UML은 다음과 같습니다.

예제 코드

예제를 살펴 보도록 하겠습니다. 여기서는 아까의 예제와 같이 낮/밤이라는 ‘상태’를 각각 클래스화하도록 할 것입니다. 그리고 낮에는 이미지 갤러리, 밤에는 뮤직 프로그램이 실행되는 프로그램을 생각해보도록 하겠습니다.

일단, 다음과 같은 인터페이스를 만들어보겠습니다.

public interface State {

  public void setTime(ContextManager cm, int hour);

  public void setItem(Item item);

  public void show();

  public void close();
}

그리고, 각 상태는 다음과 같이 구현할 수 있습니다. (여기서는 각 State를 Singleton으로 구현을 했는데, 이 부분은 자유롭게 구현해도 됩니다. 다만 잦은 State 변경에 의해서 State를 재생성해야할 경우가 많다면, State를 매번 생성해야 할 필요가 있는지는 고민해보는 것이 좋을 것 같습니다.)

public class DayState implements State {

  private static DayState mInstance = new DayState();
  private ImageGallery mImageGallery = new ImageGallery();

  private DayState() {
  }

  public static State getInstance() {
    return mInstance;
  }

  @Override
  public void setTime(ContextManager cm, int hour) {
    if((hour < 9) || (hour >= 17)) {
      cm.setState(NightState.getInstance());
    }
    cm.setTime(hour);
  }

  @Override
  public void setItem(Item item) {
    mImageGallery.setItem(item);
  }

  @Override
  public void show() {
    mImageGallery.show();
  }

  @Override
  public void close() {
    mImageGallery.close();
  }

}

public class NightState implements State {

  private static NightState mInstance = new NightState();
  private MusicLibrary mMusicLibrary = new MusicLibrary();

  private NightState() {
  }

  public static State getInstance() {
    return mInstance;
  }

  @Override
  public void setTime(ContextManager cm, int hour) {
    if((hour >= 9) && (hour < 17)) {
      cm.setState(DayState.getInstance());
    }
    cm.setTime(hour);
  }

  @Override
  public void setItem(Item item) {
    mMusicLibrary.setItem(item);
  }

  @Override
  public void show() {
    mMusicLibrary.show();
  }

  @Override
  public void close() {
    mMusicLibrary.close();
  }
}

커맨드(Command) 패턴을 살펴겠습니다. 나중에 추가로 포스팅하겠지만, 먼저 다른 패턴들과 간단히 비교하면 다음과 같습니다.

• 스테이트(State) 패턴 : 상태 그 자체를 클래스화해서 사용
• 스트래터지(Strategy) 패턴 : 알고리즘 자체를 클래스화해서 사용
• 컴포지트(Composite) 패턴 : 각 객체들을 동일시화해서 사용
• 커맨드(Command) 패턴 : 명령 그 자체를 클래스화해서 사용하는 패턴

커맨드 패턴의 UML은 다음과 같습니다.

예제 코드

커맨드 패턴의 예제는 다음과 같습니다.

public interface Command {

  public void execute();
}

이와 같은 인터페이스를 하나 구현하고, 각 명령을 구현하는 클래스들은 이 인터페이스를 구현(상속)하면 됩니다. 예를 들면 다음과 같습니다.

public class DrawCommand implements Command {

  protected Drawable mDrawable;
  private Point mPosition;

  public DrawCommand(Drawable drawable, Point position) {
    mDrawable = drawable;
    mPosition = position;
  }

  @Override
  public void execute() {
    mDrawable.draw(mPosition.x, mPosition.y);
  }
}

다음과 같이 Macro 형태의 Command도 만들 수 있습니다. Command들의 리스트를 이용하면 되는데, Stack, Queue, List 등 어떤 리스트든 성격에 따라 자유롭게 사용해도 됩니다. (여기서는 Undo, Redo 기능처럼 보이게 하기 위해 Stack을 사용했습니다.)

public class MacroHandler implements Command {

  private Stack<Command> mCommandStack = new Stack<Command>();

  @Override
  public void execute() {
    Iterator<Command> it = mCommandStack.iterator();
    while(it.hasNext()) {
      ((Command) it.next()).execute();
    }
  }

  public boolean append(Command cmd) {
    // 만약 자기 자신이 추가(append)되었을 경우 execute()에서
    // 무한 루프로 빠질 가능성이 있기 때문에 미리 확인함
    if(cmd != this) {
      mCommandStack.push(cmd);

      return true;
    }

    return false;
  }

  public void undo() {
    if(mCommandStack.empty() == false) {
      mCommandStack.pop();
    }
  }

  public void clear() {
    mCommandStack.clear();
  }
}

가장 많이 사용 되는 패턴 중 하나가 옵저버 패턴(Observer Pattern)입니다. 아마 디자인 패턴을 잘 모르더라도 자신도 모르게 이미 옵저버 패턴을 사용하고 있는 경우가 대부분일 것 같습니다. 예를 들어, 안드로이드 개발을 할 때 Button에 OnClickEventListener를 등록하는 것들이 옵저버(Observer) 패턴에 해당됩니다. 평소엔 가만히 있다가 해당 버튼이 클릭되었을 때 그 이벤트를 알려달라고 리스너를 등록하는 것입니다.

옵저버 패턴은 특정 인스턴스에 이벤트 리스너(EventListener)를 달고 대기하고 있다가 그 인스턴스에 이벤트가 발생하면 그 결과를 통보(Notify)받는 방식이며 UML로 표현하면 다음과 같습니다.

예제 코드

예제 코드는 다음과 같이 간단히 작성할 수 있습니다.

public interface Observer {

  public void update(Subject subject, int event);
}

public abstract class Subject {

  private ArrayList<Observer> mObserverList = new ArrayList<Observer>();

  public void add(Observer observer) {
    mObserverList.add(observer);
  }

  public void Remove(Observer observer) {
    mObserverList.remove(observer);
  }

  public void notify(int event) {
    for(Observer observer : mObserverList) {
      observer.update(this, event);
    }
  }
}

프로그램에서 단 하나의 인스턴스(Instance)만 존재하게 하고 싶을 때 사용하는 패턴입니다. 어디서든지 그 인스턴스에 접근할 수 있기 때문에 전역 변수 등을 관리할 때 상당히 편리하기 때문에 많은 사람들이 남발하고 있는 패턴이기도 합니다.

하지만, 싱글톤(Singleton)은 실제로는 단순 전역 변수와 거의 같은 용도로 많이 쓰이며 그 성격상 객체 지향과는 거리가 있는 패턴입니다. 프로그램 어느 곳에서든 Singleton에 접근할 수 있기 때문에 정보의 보호도 되지 않으며, 누가 어떤 값을 건드렸는지 추적하기도 쉽지 않습니다. 따라서 가급적 사용하지 않는 것이 좋지만 적절하게 제한적을 사용하면 편리하긴 합니다.

#UML

싱글톤 패턴의 UML은 다음과 같습니다. 클래스 하나 뿐이기 때문에 UML이 단순합니다.

예제 코드

싱글톤 패턴을 코드로 구현하면 다음과 같습니다. (다만, 이 코드는 멀티쓰레드(Multi-Thread) 환경에서 문제가 발생하는 코드입니다. 해결법이 여러가지인데, 단계별로 해결된 코드를 설명해나가도록 하겠습니다.)

public class Singleton {

  private static Singleton mInstance = null;

  private Singleton() {
  }

  public static Singleton getInstance() {
    if(mInstance == null) {
      mInstance = new Singleton();
    }

    return mInstance;
  }
}

위 코드는 멀티쓰레드 환경에서 getInstace() 메소드가 끝나기 전에 여러 쓰레드에서 동시에 접근을 할 수 있기 때문에 재수가 없으면 Singleton 인스턴스가 여러 개 생성될 수 있습니다.

함수 전체에 synchronized 적용

이 경우 getInstance() 메소드를 synchronized로 동기화시켜 해결할 수 있습니다.

public class Singleton {

  private static Singleton mInstance = null;

  private Singleton() {
  }

  public synchronized static Singleton getInstance() {
    if(mInstance == null) {
      mInstance = new Singleton();
    }

    return mInstance;
  }
}

하지만, 함수 전체에 synchronized는 동기화 과정에서 속도 문제가 발생하고 성능 저하를 가져 올 수 있습니다. (물론, 위 예제 코드 정도로는 그렇게 치명적인 속도 문제가 발생할 가능성은 많지 않습니다.)

함수 내부 일부분에 synchronized 적용

그래서 함수 내부에 최소 구간에만 synchronized를 거는 방법도 있습니다.

public class Singleton {

  private static Singleton mInstance = null;

  private Singleton() {
  }

  public static Singleton getInstance() {
    if(mInstance == null) {
      synchronized(Singleton.class) {
        if(mInstance == null) {
          mInstance = new Singleton();
        }
      }
    }

    return mInstance;
  }
}

처음부터 인스턴스를 생성

그리고 코드를 좀 더 깔끔하고 쉽게 구현하기 위해서는 아예 처음부터 인스턴스를 생성해버리는 방법도 있습니다. 저는 처음부터 인스턴스를 생성하는 방법을 가장 많이 사용하고 있습니다. 구현도 쉽고 코드도 더 깔끔한 것 같아서입니다.

public class Singleton {

  private static Singleton mInstance = new Singleton();

  private Singleton() {
  }

  public static Singleton getInstance() {
    return mInstance;
  }
}

물론 이 경우는 프로그램이 처음 실행되면서 바로 인스턴스가 생겨버리기 때문에, 불필요한 부분에서 인스턴스가 메모리를 차지해버린다는 단점이 있습니다. 하지만, 그런 경우는 Singleton을 사용하지 않는게 더 적합한 경우가 많기 때문에 대부분의 Singleton 구현은 위의 마지막 예제처럼 구현하면 됩니다.

하지만 최선은 싱글톤 패턴을 사용하지 않거나 최소한으로 사용하는 거라고 생각합니다.